Clojure> programming-clojure-ch5

June 26th, 2017 - CREATED

함수형 프로그래밍

함수형 프로그래밍의 개념

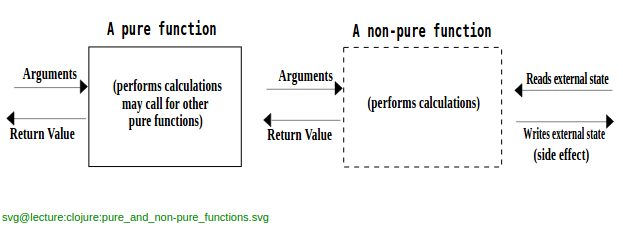
순수함수

함수형 프로그램은 ‘순수 함수’로 이루어져 있다. ‘부수효과’가 전혀 없는 함수를 말한다.
오로지 인자에만 의존해서 결과가 만들어지고, 반환 값으로만 외부 세계에 영향을 준다.

영속적 자료구조

‘변경 불가능 데이터(immutable data)’는 클로저의 함수형 프로그래밍과 병행 프로그래밍 방식에 매우 중요한 요소다.
병행 프로그래밍 측면에서 스레드 안전성(thread-safety)를 보장하기 위해 변경 불가능한 자료구조가 필요하게 된다.
문제 –> 모든 데이터가 immutable 하다면, 데이터 ‘갱신’이란 곧 ‘기존 데이터에 변화가 가해진 새로운 데이터를 ‘생성’ 한다는 뜻 –> 메모리 소모가 커짐.
클로저의 자료구조는 이러한 ‘모든 것을 복사하는’ 방식을 취하지 않는다.
클로저의 자료구조는 ‘영속적(persistent)’이다. -> 갱신전의 데이터와 후의 데이터가 변경되느 않은 부분을 그대로 ‘공유하는’ 효율적인 접근 방식을 취한다.
example
```
user> (def a '(1 2 3))
user> (def b (cons 0 a))
```
–> b는 a 전체를 복사하는 대신 다음과 같이 a를 그대로 사용한다.
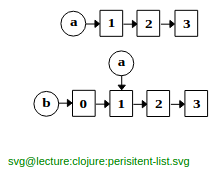
클로저의 모든 자료구조는 가능한 한 자료구조를 공유하는 방식을 택한다.

지연 평가와 재귀

함수형 프로그래밍은 ‘재귀’와 ‘지연 평가’를 매우 많이 사용한다.
함수와 표현식에 대해서는 기본적으로 평가가 지연되지 않는다. 그러나 시퀀스에 대해서는 평가를 지연한다.
지연 평가를 이용하는 기법은 사실 순수 함수 사용을 전제로 한다. –> 순수 함수를 사용한다면 함수의 호출 시점과 결과는 차이가 없기 때문이다.

참조 투명성

지연 평가는 기본적으로 함수 호출을 그 호출의 결과로 치환해도 결과가 같다는 전제에 의존하고 있다.
함수 호출 자체를 함수의 결과로 치환해도 프로그램의 행동에 영향을 미치지 않는 함수를 가리켜 ‘참조 투명성(referential transparency) 이 있는 함수’라고 한다.
–> ‘메모이제이션(memoization)’을 사용할 수 있다. : 함수의 반환 값을 자동으로 캐싱하는 기법
–> ‘병행성’을 저절로 확보하게 된다.
순수함수는 기본적으로 참조 투명성을 가진다.

함수형 프로그래밍의 이점

함수를 작성하는 데 필요한 모든 정보가 함수 인자에 있기 때문에 ‘작성’이 쉽다. –> ‘읽기’도 쉽다.
테스트를 위해 만들어야 할 환경은 함수의 인자뿐이다.
캡슐화의 원칙을 철저히 지키며, 조합을 쉽게 만든다. 순수 함수를 시스템의 어디에 끼워넣든간에 그것들은 항상 같은 방식으로 작동한다.

여섯 가지 원칙

직접 재귀를 사용하는 것을 피하자. JVM이 tail-call optimization 을 하지 못하기 때문에, 직접 재귀를 사용하면 순식간에 스택을 소모하게 된다.
대신 recur 을 사용하자. recur는 무한이 아닌, 작은 규모의 시퀀스를 만들 때 사용하는 것이 좋다.
규모가 큰 시퀀스를 만들때는 지연 시퀀스로 만든다. 연산 비용이 작아진다.
지연 시퀀스에서 실제로 필요한 부분 이외의 것까지 평가하지 않도록 주의한다.
시퀀스 라이브러리를 이용하자.
쪼개서 정복하자. 더 작은 구성 요소로 쪼개면 시퀀스 라이브러리 같은 범용적이고 재사용 가능한 코드로 문제를 해결 할 수 있다.

연산의 지연

재귀적 정의

기저(basis) : 만들어 내려는 시퀀스 가운데 추론이 필요 없는 매우 명백한 원소
귀납 규칙 : 기저를 바탕으로 추가적 원소를 만들어 내는 데 필요한 규칙
기본적 재귀 : 함수가 자기 자신을 호출하게 한 뒤 적절한 조작을 가해, 귀납에 해당하는 과정을 만들어 내는 방법
꼬리 재귀 : 함수가 함수 정의의 마지막 부분에서 자기 자신을 호출하는 것외에 다른 조작을 가하지 않는 형태. –> ‘꼬리 재귀 최적화’로 불리는 성능 최적화가 가능해진다.
지연 시퀀스 : 실제로 재귀 과정을 실행하기보다, 지연 시퀀스를 이용해서 값이 정말로 필요해질 때 계산하는 방법
example : 피보나치 수열 (0 1 1 2 3 5 8 13 21 34 … )

bad case

user> (defn stack-consuming-fibo [n]
     (cond
       (= n 0) 0
       (= n 1) 1
       :else (+ (stack-consuming-fibo (- n 1))
                (stack-consuming-fibo (- n 2)))))
#'user/stack-consuming-fibo
user> (stack-consuming-fibo 9)
34
user> (stack-consuming-fibo 9000)
StackOverflowError   clojure.lang.Numbers$LongOps.combine (Numbers.java:419)
==> stack overflow 유발 시킴
==> stack-consuming-fibo를 호출할 때마다 stack-consuming-fibo 에 대한 호출이 두 개씩 더 생겨나게 된다.
==> '스택 프레임'이 계속 쌓이게 된다.

꼬리 재귀 stack-consuming-fibo는 함수를 호출한 뒤에 더하기(+) 함수를 호출하므로 꼬리 재귀라고 할 수 없다. 함수의 인자가 다음 귀납 과정을 수행하는 데 충분한 정보를 지니도록 만들어 주면 된다. 여기서는 n 이 된다.

user> (defn tail-fibo [n]
     (letfn [(fib
               [current next n]     ; current, 다음, 결과를 내기까지 남은 단계의 숫자 n
               (if (zero? n)
                 current
                 (fib next (+ current next) (dec n))))]
       (fib 0 1 n)))
#'user/tail-fibo
user> (tail-fibo 9)
34
user> (tail-fibo 9000)
ArithmeticException integer overflow  clojure.lang.Numbers.throwIntOverflow (Numbers.java:1501)
==> letfn 은 지역함수를 바인딩한다. letfn 에서 선언된 함수는 자기 자신을 부를 수 있고 letfn 블록 내에 정의된 다른 함수를
호출할 수도 있다.
==> JVM에서 직접 돌아가는 어떤 언어도 자동적인 꼬리 최적화를 수행하지 못한다.

recur를 이용한 자체 재귀

user> (defn recur-fibo [n]
     (letfn [(fib
               [current next n]
               (if (zero? n)
                 current
                 (recur next (+ current next) (dec n))))]
       (fib 0 1 n)))
#'user/recur-fibo
user> (recur-fibo 9000)
ArithmeticException integer overflow  clojure.lang.Numbers.throwIntOverflow (Numbers.java:1501)

==> 이상함… 안됨. ==> 하나의 fibo 값만 구한다. 그렇다면 이전에 계산한 피보나치 수를 추후의 필요를 위해 캐싱한다고 할 때 ???

지연 시퀀스 lazy-seq 라는 매크로를 이용한다. 함수 호출의 재귀적인 부분을 lazy-seq로 감싸서 재귀적 호출을 지연할 필요가 있다.

user> (defn lazy-seq-fibo
     ([]
      (concat [0 1] (lazy-seq-fibo 0 1)))
     ([a b]
      (let [n (+ a b)]
        (lazy-seq
         (cons n (lazy-seq-fibo b n))))))
#'user/lazy-seq-fibo
user> (take 10 (lazy-seq-fibo))
(0 1 1 2 3 5 8 13 21 34)

Language (25)

kchhero

If you do not act, there is no change.